
臺大管理論叢
第
27
卷第
3
期
73
(20)
對於一個帶有
p
個自變數的迴歸模型,以
k
個代理變數所進行的正交轉換,得到
第一個自變數的相對權數定義如方程式
(21)
所示,
RIW
係數運算所涉及的各係數關係
如圖
1
所示。
(21)
從方程式
(20)
與
(21)
可知,
RIW
係數主要是由兩組與代理變數
Z
有關的轉換係
數
λ
(由
Z
k
→
X
j
)與
β
(由
Z
k
→
Y
)所構成,將 進行加總可得出屬於各
IV
對於
依變數
Y
進行解釋的變異數比例。
Y
X
1
Z
1
X
2
Z
2
X
p
Z
k
e
1
v
λ
11
λ
21
λ
22
λ
12
λ
1
k
λ
PK
λ
P
1
λ
P
2
λ
2
P
β
1
β
2
β
k
e
2
e
p
...
...
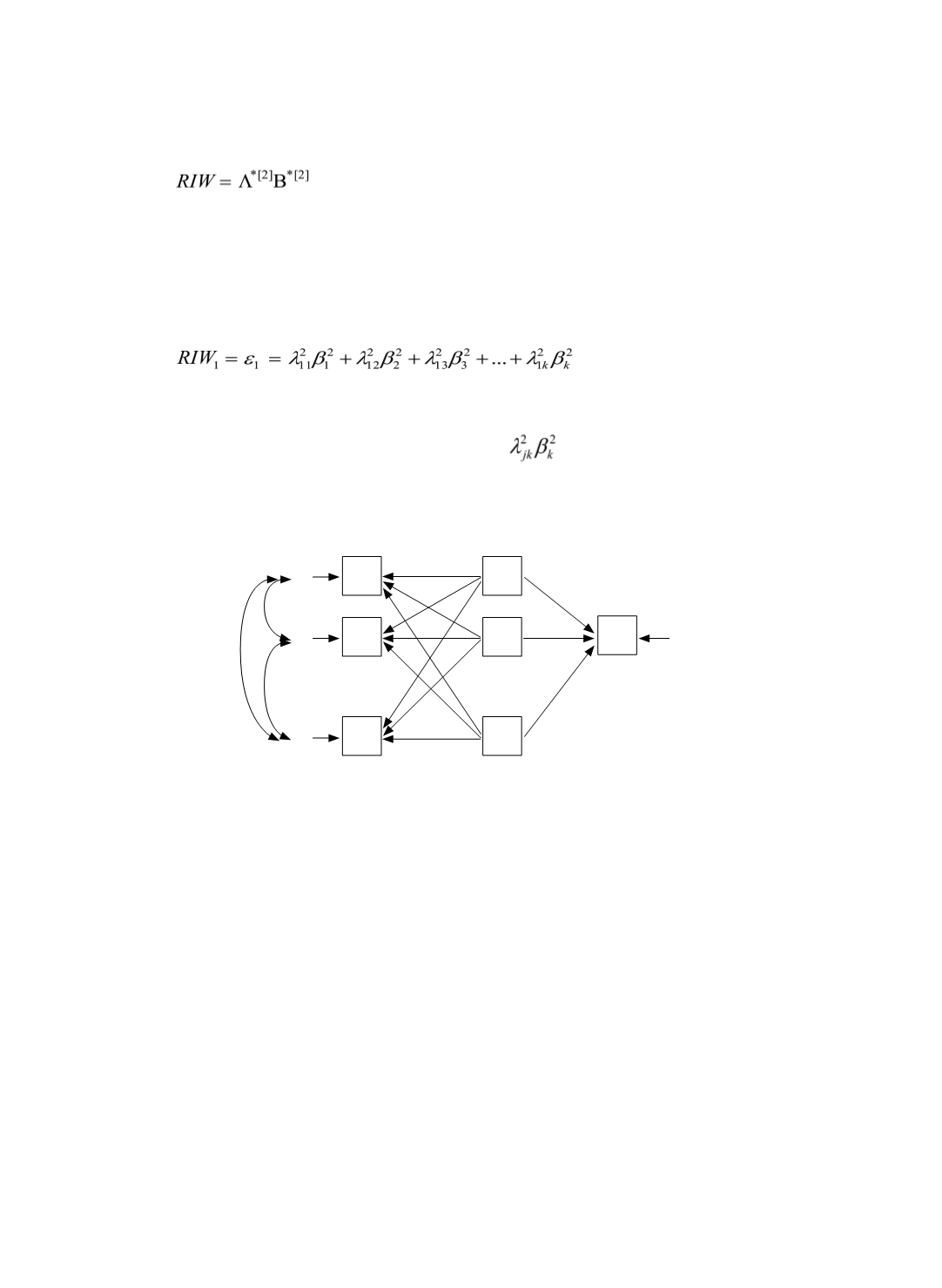
(修改自
Tonidandel, LeBreton, and Johnson (2009), p.390, Figure1
)
圖
1
帶有
p
個自變數的
RIW
係數運算過程圖示
RIW
係數的演算程序與乘積指數類似,且
RIW
係數的總和等於整體模式解釋
力,亦即
ΣRIW =
R
2
,使得
RIW
係數能對
R
2
進行正交分割而保持整體模型解釋力在
固定的基準上,若將各
IV
的
RIW
係數除以
R
2
,得到重新量尺化重要權數
(Rescaled
Importance Weights)
,亦即各
IV
分割
R
2
的比例(各
IV
的正交化解釋百分比)。
對於
RIW
係數的統計意義,
Tonidandel et al. (2009)
發展出以拔靴程序為基礎的顯
著性檢定法,除了能夠檢驗
RIW
係數是否顯著不為零的
NHST
,也可建立
95%
信賴
區間來進行
RIW
係數的差異比較。但是在小樣本(例如
n
< 30
)時即使以拔靴標準誤
進行討論仍會有偏誤產生,因此必須在有相當充分樣本規模時才採用
(Tonidandel and
LeBreton, 2011)
。經過模擬研究(例如
LeBreton, Ployhart, and Ladd, 2004; LeBreton and


















