
臺大管理論叢
第
27
卷第
3
期
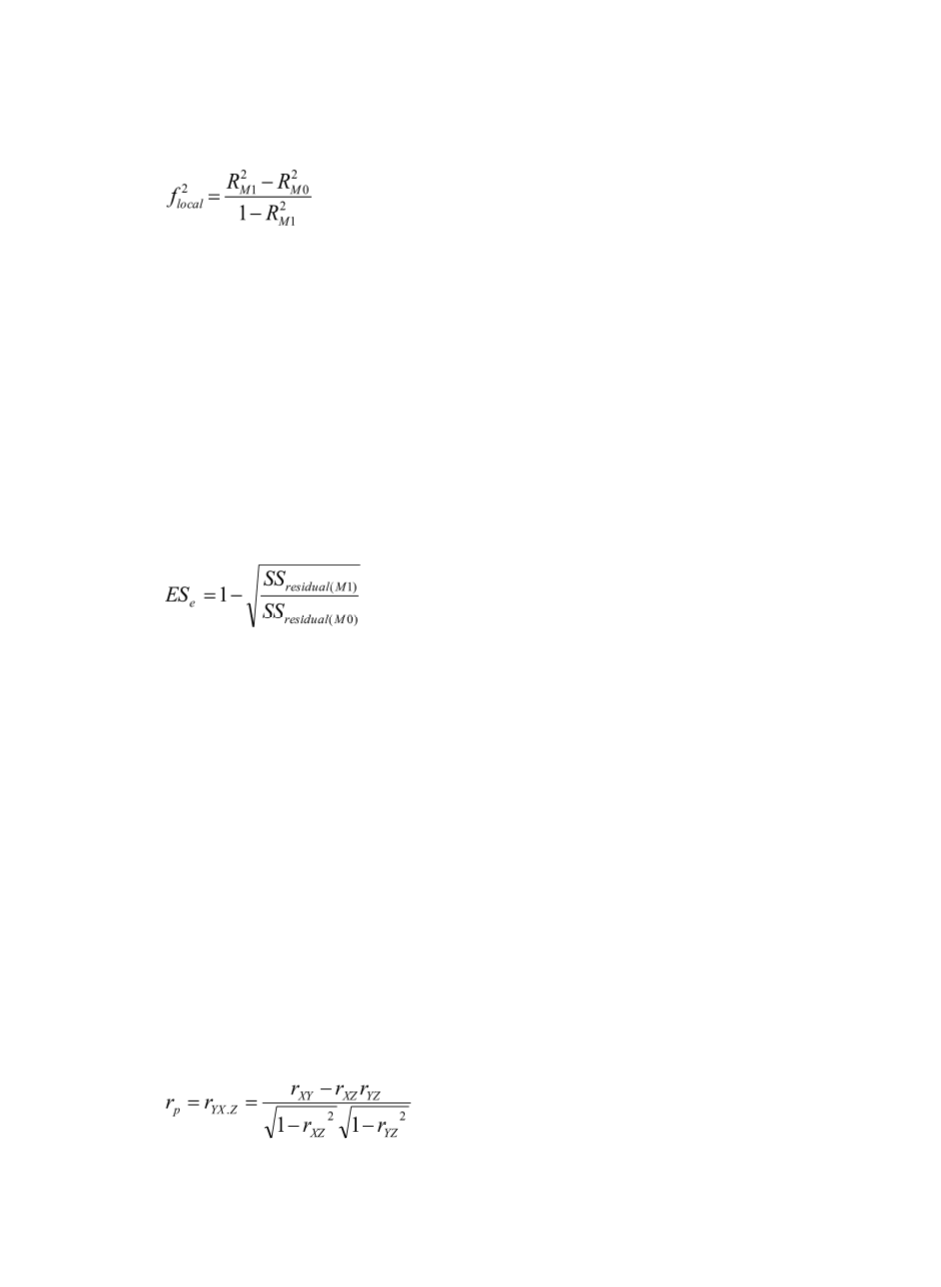
69
(6)
其中
R
2
M
0
為帶有
k
個
IV
的基準模型
(M0)
的解釋變異,
R
2
M
1
為投入額外一個或多
個
IV
後的新模型
(M1)
的解釋變異,因此
f
2
local
統計量可視為增量效果。
(四)殘差削減效果量
R
2
所關注的是全體
IV
對於
DV
變異的解釋力,相對之下,殘差削減法則是以殘
差變異為焦點,探討投入
IV
對於迴歸殘差的影響
(Berry and Mielke, 2002)
。利用殘差
削減
(Proportional Reduction in Error; PRE)
的概念,當越多的
IV
投入方程式,殘差變
異降低越多,當某個已帶有
k
個
IV
的迴歸模型作為參照模型
(M0)
,若額外再多投入
一個或多個
IV
作為比較模型
(M1)
,
M1
的殘差變異必然小於
M0
,因而得以導出一個
改善比效果量
(
ES
e
)
,如方程式
(7)
所示。
(7)
由於增加
IV
時的殘差變異為單調遞減,因此
ES
e
數值介於
0
至
1
間,數值越大
表示新增的
IV
解釋力越強。而且由於
ES
e
為不同模型的殘差比值,因此也類似於調
整後
R
2
,並無相對應的抽樣標準誤得以進行顯著性檢定,但可利用拔靴法來建立信賴
區間以進行比較
(Preacher and Kelley, 2011)
。
二、個別效果量指標
(一)以積差相關為基礎的指標
為瞭解個別
IV
對於
DV
的影響程度,最直接的方法就是觀察
X
與
Y
兩者間的相
關係數
r
XY
。相關越高表示兩者關係越強,而且
r
XY
為標準化係數,因此可相互比較。
但由於相關係數僅考慮了
X
與
Y
兩變數間的關係,完全不考慮模型當中所存在的其
他變數,因此稱為零階相關
(Zero-order Correlation)
。如果要將其他
IV
(以
Z
表示)
的效果移除,可以採取淨相關
(Partial Correlation;
r
p
)
(方程式
(8)
)或半淨相關
(Semipartial Correlation;
r
sp
)
(方程式
(9)
)
:
(8)


















